Read a Float Varilable With Three Decimal Points

Anti-intuitive 🥸 but yet interactive example of how the floating-betoken numbers similar -27.156 are stored in binary format in a calculator'due south retentiveness

Jolly photo by Daniel Lanner

Have yous ever wondered how computers store the floating-bespeak numbers like 3.1416 (𝝿) or 9.109 × x⁻³¹ (the mass of the electron in kg) in the retentivity which is limited by a finite number of ones and zeroes (aka bits)?

It seems pretty straightforward for integers (i.e. 17). Allow'due south say nosotros accept 16 bits (2 bytes) to shop the number. In xvi bits we may shop the integers in a range of [0, 65535]:

              (0000000000000000)₂ = (0)₁₀  (0000000000010001)₂ =     (i × 2⁴) +     (0 × 2³) +     (0 × 2²) +     (0 × 2¹) +     (i × 2⁰) = (17)₁₀  (1111111111111111)₂ =     (1 × 2¹⁵) +     (one × two¹⁴) +     (ane × 2¹³) +     (1 × 2¹²) +     (1 × 2¹¹) +     (1 × 2¹⁰) +     (1 × ii⁹) +     (1 × 2⁸) +     (ane × two⁷) +     (1 × 2⁶) +     (1 × ii⁵) +     (1 × 2⁴) +     (1 × ii³) +     (1 × two²) +     (1 × 2¹) +     (one × 2⁰) = (65535)₁₀            

If we need a signed integer we may apply two'south complement and shift the range of [0, 65535] towards the negative numbers. In this case, our 16 $.25 would represent the numbers in a range of [-32768, +32767].

Every bit you might have noticed, this arroyo won't allow you to represent the numbers like -27.15625 (numbers after the decimal point are but being ignored).

We're not the first ones who have noticed this issue though. Around ≈36 years ago some smart folks overcame this limitation by introducing the IEEE 754 standard for floating-point arithmetic.

The IEEE 754 standard describes the style (the framework) of using those 16 $.25 (or 32, or 64 bits) to store the numbers of wider range, including the small floating numbers (smaller than one and closer to 0).

To become the thought behind the standard we might recall the scientific notation - a way of expressing numbers that are as well big or besides minor (usually would result in a long cord of digits) to exist conveniently written in decimal course.

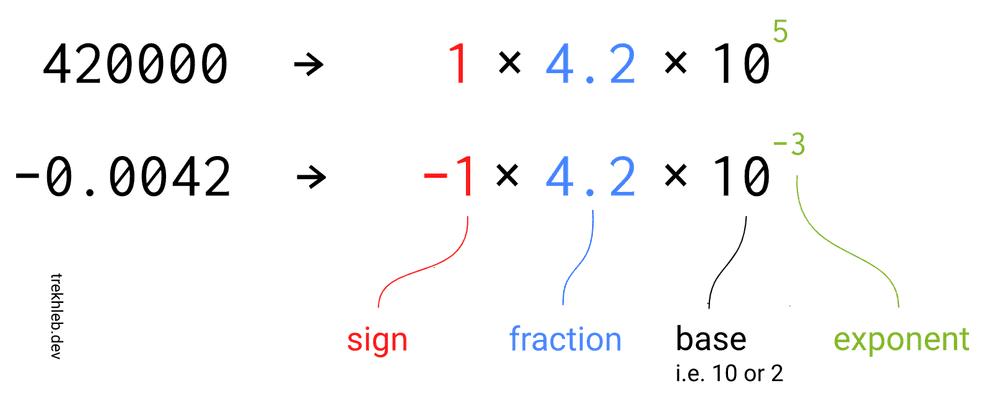
As you may see from the image, the number representation might exist split into iii parts:

• sign
• fraction (aka significand) - the valuable digits (the significant, the payload) of the number
• exponent - controls how far and in which direction to move the decimal indicate in the fraction

The base office we may omit by just like-minded on what it volition be equal to. In our case, we'll be using 2 as a base of operations.

Instead of using all xvi bits (or 32 bits, or 64 bits) to store the fraction of the number, we may share the bits and store a sign, exponent, and fraction at the same time. Depending on the number of bits that we're going to utilize to shop the number nosotros terminate upwards with the following splits:

Floating-betoken format	Total bits	Sign bits	Exponent bits	Fraction bits	Base
Half-precision	16	1	5	10	2
Single-precision	32	one	8	23	2
Double-precision	64	one	11	52	2

With this arroyo, the number of bits for the fraction has been reduced (i.e. for the 16-bits number it was reduced from 16 bits to 10 bits). It means that the fraction might accept a narrower range of values now (losing some precision). However, since we also have an exponent part, it volition actually increase the ultimate number range and also permit us to describe the numbers between 0 and 1 (if the exponent is negative).

For example, a signed 32-bit integer variable has a maximum value of 2³¹ − 1 = two,147,483,647, whereas an IEEE 754 32-bit base-2 floating-point variable has a maximum value of ≈ 3.4028235 × 10³⁸.

To brand it possible to take a negative exponent, the IEEE 754 standard uses the biased exponent. The thought is simple - subtract the bias from the exponent value to make it negative. For instance, if the exponent has 5 bits, information technology might take the values from the range of [0, 31] (all values are positive here). But if we subtract the value of 15 from it, the range volition be [-xv, 16]. The number 15 is called bias, and it is being calculated by the following formula:

              exponent_bias = 2 ^ (k−i) − 1  k - number of exponent bits            

I've tried to draw the logic backside the converting of floating-signal numbers from a binary format back to the decimal format on the image below. Hopefully, it will requite you a better understanding of how the IEEE 754 standard works. The 16-bits number is existence used here for simplicity, but the aforementioned approach works for 32-bits and 64-bits numbers likewise.

Hither is also the interactive tool to give you lot improve intuition of how the conversion works. Feel gratis to flip some bits and see how it affects the final formula.

👉🏻 One-half-precision (16 bits) floating indicate format

Be aware that this is by no means a complete and sufficient overview of the IEEE 754 standard. It is rather a simplified and basic overview. Several corner cases were omitted in the examples above for simplicity of presentation (i.e. -0, -∞, +∞ and NaN (not a number) values)

Hither is the number ranges that different floating-betoken formats back up:

Floating-point format	Exp min	Exp max	Range	Min positive
Half-precision	−fourteen	+15	±65,504	6.ten × ten⁻⁵
Unmarried-precision	−126	+127	±three.4028235 × 10³⁸	1.xviii × 10⁻³⁸

Code examples

In the javascript-algorithms repository, I've added a source code of binary-to-decimal converters that were used in the interactive example above.

Below you lot may find an instance of how to get the binary representation of the floating-point numbers in JavaScript. JavaScript is a pretty high-level language, and the example might be as well verbose and non as straightforward as in lower-level languages, but however it is something you may experiment with direct in the browser:

                              const                singlePrecisionBytesLength                =                four                ;                // 32 bits                const                doublePrecisionBytesLength                =                viii                ;                // 64 $.25                const                bitsInByte                =                8                ;                /**  * Converts the float number into its IEEE 754 binary representation.  * @see: https://en.wikipedia.org/wiki/IEEE_754  *  * @param {number} floatNumber - float number in decimal format.  * @param {number} byteLength - number of bytes to utilize to store the bladder number.  * @return {cord} - binary string representation of the float number.  */                function                floatAsBinaryString                (                floatNumber,                  byteLength                )                {                let                numberAsBinaryString                =                ''                ;                const                arrayBuffer                =                new                ArrayBuffer                (byteLength)                ;                const                dataView                =                new                DataView                (arrayBuffer)                ;                const                byteOffset                =                0                ;                const                littleEndian                =                false                ;                if                (byteLength                ===                singlePrecisionBytesLength)                {                dataView.                setFloat32                (byteOffset,                floatNumber,                littleEndian)                ;                }                else                {                dataView.                setFloat64                (byteOffset,                floatNumber,                littleEndian)                ;                }                for                (                let                byteIndex                =                0                ;                byteIndex                <                byteLength;                byteIndex                +=                1                )                {                let                bits                =                dataView.                getUint8                (byteIndex)                .                toString                (                2                )                ;                if                (bits.length                <                bitsInByte)                {                bits                =                new                Assortment                (bitsInByte                -                $.25.length)                .                make full                (                '0'                )                .                join                (                ''                )                +                bits;                }                numberAsBinaryString                +=                bits;                }                render                numberAsBinaryString;                }                /**  * Converts the bladder number into its IEEE 754 64-bits binary representation.  *  * @param {number} floatNumber - float number in decimal format.  * @return {string} - 64 bits binary cord representation of the float number.  */                part                floatAs64BinaryString                (                floatNumber                )                {                return                floatAsBinaryString                (floatNumber,                doublePrecisionBytesLength)                ;                }                /**  * Converts the bladder number into its IEEE 754 32-bits binary representation.  *  * @param {number} floatNumber - float number in decimal format.  * @return {string} - 32 bits binary cord representation of the float number.  */                function                floatAs32BinaryString                (                floatNumber                )                {                return                floatAsBinaryString                (floatNumber,                singlePrecisionBytesLength)                ;                }                // Usage case                floatAs32BinaryString                (                1.875                )                ;                // -> "00111111111100000000000000000000"                          

References

You might also desire to check out the following resources to get a deeper agreement of the binary representation of floating-point numbers:

• Hither is what you lot demand to know most JavaScript'southward Number type
• Float Exposed
• IEEE754 Visualization

shecklerhavess.blogspot.com

Source: https://trekhleb.dev/blog/2021/binary-floating-point/

Share this post